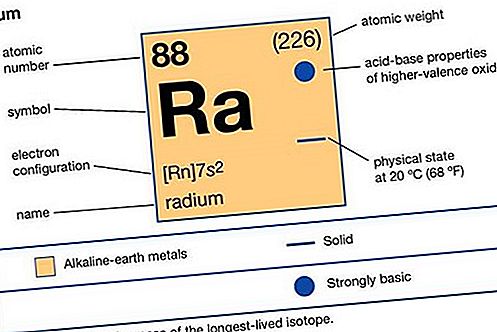
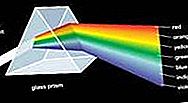
Kónický řez, také nazývaný kónický, v geometrii jakákoli křivka vytvořená průnikem roviny a pravého kruhového kužele. V závislosti na úhlu roviny vzhledem k kuželu je průsečíkem kružnice, elipsa, hyperbola nebo parabola. Zvláštní (degenerované) případy průniku nastávají, když rovina prochází pouze vrcholem (vytváří jediný bod) nebo vrcholem a dalším bodem na kuželu (vytváří jednu přímku nebo dvě protínající se přímky). Podívejte se na obrázek.
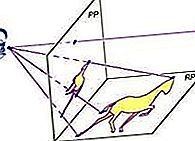
projektivní geometrie: Projektivní kuželové řezy
Kónické řezy lze považovat za rovinné řezy pravého kruhového kužele (viz obrázek). Pokud jde o
Základní popisy, nikoli však názvy, kuželových sekcí lze vysledovat až po Menaechmus (vzkvétal cca 350 př. Nl), žáka Plata i Eudoxuse z Cnidusu. Apollonius z Pergy (c. 262–190 př. Nl), známý jako „Velký geometr“, dal kónickým řezům svá jména a jako první definoval dvě větve hyperboly (které předpokládají dvojitý kužel). Apolloniusova osmidílná pojednání o kuželovitých sekcích, Conics, je jednou z největších vědeckých prací ze starověkého světa.
Analytická definice
Kónické tvary mohou být také popsány jako rovinné křivky, které jsou cestami (loci) bodu pohybujícího se tak, že poměr jeho vzdálenosti od pevného bodu (fokus) k vzdálenosti od pevné linie (directrix) je konstanta, nazývaná excentricita křivky. Pokud je excentricita nula, je křivka kružnicí; pokud se rovná jedné, parabola; pokud je méně než jedna, elipsa; a pokud je více než jedna, hyperbola. Podívejte se na obrázek.
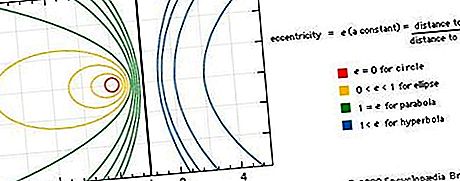
Každý kónický řez odpovídá grafu druhé stupně polynomické rovnice tvaru Ax 2 + 2 + 2Cxy + 2Dx + 2Ey + F = 0, kde xay jsou proměnné a A, B, C, D, E a F jsou koeficienty, které závisí na konkrétním kónusu. Vhodnou volbou souřadných os lze rovnici pro každý kónický tvar redukovat na jednu ze tří jednoduchých r tvarů: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1, nebo y 2 = 2px, odpovídající elipsě, hyperbole a parabole. (Elipsa, kde a = b je ve skutečnosti kruh.) Rozsáhlé použití souřadnicových systémů pro algebraickou analýzu geometrických křivek vzniklo u René Descartes (1596–1650). Viz Historie geometrie: Kartézská geometrie.
Řecký původ
Raná historie kuželovitých sekcí je spojena s problémem „zdvojnásobení krychle“. Podle Eratosthenes z Cyrene (c. 276–190 př. Nl) lidé Delosu konzultovali věštce Apolla o pomoc při ukončení moru (asi 430 př. Nl) a byli pověřeni, aby postavili Apollo nový oltář dvojnásobného objemu starého oltáře. a se stejným tvarem krychlové. Delianové se zmateně radili s Platónem, který prohlásil, že „věštec neznamenal, že bůh chtěl oltář dvojnásobné velikosti, ale že si přál, aby jim při určování úkolu zahanbil Řeky za jejich zanedbávání matematiky a jejich pohrdání pro geometrii. “ Hippokrates of Chios (c. 470–410 bc) nejprve zjistil, že „Delianův problém“ lze redukovat na nalezení dvou středních proporcí mezi a a 2a (objemy příslušných oltářů) - to znamená, že určíme xay tak, že: x = x: y = y: 2a. Toto je ekvivalent k řešení současně jakékoliv dvě z rovnic x 2 = ay, y 2 = 2AX a xy = 2a 2, které odpovídají dvěma parabolami a hyperboly, resp. Později Archimedes (c. 290–211 bc) ukázal, jak pomocí kónických řezů rozdělit kouli na dva segmenty s daným poměrem.
Diokle (c. 200 bc) geometricky demonstroval, že paprsky - například ze Slunce -, které jsou rovnoběžné s osou rotačního paraboloidu (vytvářeného otáčením paraboly kolem její osy symetrie), se setkávají při zaostření. Archimedes je řekl, aby použil tuto vlastnost k zapálení nepřátelských lodí. Fokální vlastnosti elipsy citoval Anthemius z Tralles, jeden z architektů katedrály Hagia Sophia v Konstantinopoli (dokončen v roce 537), jako prostředek k zajištění toho, aby oltář mohl být celý den osvětlen slunečním světlem.