Neelastická odpověď
Výše uvedený způsob vyjádření [σ] ve smyslu [S] platí pro pevné látky vykazující také viskoelastickou nebo plastickou odezvu, s tou výjimkou, že [S] je pak třeba považovat nejen za funkci přítomného [E M] a θ, ale také v závislosti na předchozí historii obou. Za předpokladu, že takové materiály vykazují elastickou reakci na náhlé změny napětí nebo na malé vyložení z plasticky deformujícího stavu, může být [S] stále vyjádřeno jako derivát f, jak je uvedeno výše, ale derivát se chápe jako odebraný s ohledem na elastickou kolísání deformace a musí být učiněno při pevné θ as pevnou předchozí nepružnou deformací a teplotní historií. Taková závislost na historii je někdy představována jako závislost f na vnitřních stavových proměnných, jejichž evoluční zákony jsou součástí nepružného konstitutivního popisu. Existují také jednodušší modely nepružné odezvy a dále jsou uvedeny nejčastěji používané formy plasticity a tečení v izotropních pevných látkách.
K dobré aproximaci způsobuje plastická deformace krystalických pevných látek žádnou změnu objemu; a hydrostatické změny napětí, rovnající se stejné změně všech normálních napětí, nemají žádný vliv na plastický tok, přinejmenším na změny, které jsou stejného řádu nebo velikosti jako pevnost pevné látky ve smyku. Plastická odezva je tedy obvykle formulována jako deviátorové napětí, které je definováno τ ij = σ ij - δ ij (σ 11 + σ 22 + σ 33) / 3. Podle Richarda von Misese, v proceduře, která je shledána, že souhlasí s experimentem mírně dobře, je vztah plastického toku formulován jako druhý invariant deviátorového stresu, běžně přepisovaný jako
a nazvali ekvivalentní napětí v tahu. Definice je provedena tak, že pro stav jednoosého napětí σ se rovná tahovému napětí a vztah napětí-napětí pro obecné stavy napětí je formulován na základě údajů z tahového testu. Zejména je plastické napětí ε p v testu jednoosého napětí definováno z ε p = ε - σ / E, kde ε je interpretováno jako napětí v tahové zkoušce podle logaritmické definice ε = lnλ, modul pružnosti E je předpokládá se, že se nezmění s deformací, a σ / E << 1.
Ve verzi teorie plasticity nezávislé na rychlosti se tedy předpokládá, že tahová data (nebo kompresivní, s příslušným obrácením znaménka) z testu monotónní zátěže definují funkci ε p (σ). Ve viskoplastických nebo vysokoteplotních creepových verzích teorie jsou tahová data interpretována tak, aby definovala dε P / dt jako funkci σin nejjednoduššího případu, představujícího například sekundární creep, a jako funkci σ a ε p v teoriích určené k tomu, aby představovaly přechodné účinky tečení nebo odezvu citlivou na rychlost při nižších teplotách. Vezměme nejprve model tuhého plastu, u kterého je elastická deformovatelnost zcela ignorována, jak je někdy vhodné pro problémy s velkým tokem plastu, jako při formování kovu nebo dlouhodobém tečení v zemském plášti nebo pro analýzu zatížení plastů při kolapsu struktur. Rychlost deformačního tenzoru D ij je definována pomocí 2D ij = ∂v i / ∂x j + ∂v j / ∂x i, a v případě tuhého plastu [D] lze přirovnat k tomu, co lze považovat za jeho plastovou část [D p], vzhledem k tomu, jako D p / ij = 3 (dε p / dt) τ ij / 2σ. Numerické faktory zajistit dohodu mezi D p / 11 a dε p / dt na jednoosém napětí v 1direction. Rovnice to také znamená
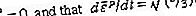
která musí být integrována do předchozí historie, aby se získala ε p, jak je požadováno pro viskoplastické modely, ve kterých dε p / dt je funkcí σ a ε p. Ve verzi nezávislé na rychlosti je [D p] definována jako nula, kdykoli σ je menší než nejvyšší hodnota, kterou dosáhla v předchozí historii, nebo když aktuální hodnota σ je nejvyšší hodnota, ale dσ / dt <0. (V kontextu elastického plastu to znamená, že „vykládka“ zahrnuje pouze elastickou odezvu.) Pro ideálně plastickou hmotu, která je idealizovaná, aby mohla proudit bez zvýšení napětí, když σ odpovídá úrovni meze kluzu, dε p / dt je považován za neurčitý, ale nutně nezáporný parametr, který lze určit (někdy ne jedinečně) pouze prostřednictvím úplného řešení problému mezní hodnoty pevné mechaniky.
Model pružně plastického materiálu je potom formulován psáním Dj = D e / ij + D p / ij, kde D p / ij je dáno jako napětí a možná míra napětí, jak je uvedeno výše, a kde jsou hodnoty elastické deformace [D e] se vztahují ke stresům obvyklým lineárním elastickým výrazem D e / ij = (1 + ν) σ ij * / E - νδ ij (σ 11 * + σ 22 * + σ 33 *) / E. Zde jsou míry stresu vyjádřeny jako Jaumannovy ko-rotační rychlosti

je derivát, který sleduje pohyb hmotného bodu a kde je rotace Ω ij definována pomocí 2Ω ij = ∂v i / ∂x j - ∂v j / ∂x i. Hodnoty ko-rotačního napětí jsou ty, které vypočítává pozorovatel, který se točí s průměrnou úhlovou rychlostí materiálového prvku. Elastická část vztahu napětí-napětí by měla být v souladu s existencí volné energie f, jak bylo diskutováno výše. To není striktně splněno právě danou formou, ale rozdíly mezi ní a jednotnou, která je takto konzistentní, zahrnují dodatečné termíny, které jsou řádově σ / E 2 krát σ kl * a jsou zanedbatelné v typických případech, kdy teorie se používá, protože σ / E je obvykle extrémně malý zlomek jednoty, řekněme 10–4 až 10 −2. Verze s malým napětím teorie se běžně používá pro účely analýzy elasticko-plastického napětí. V těchto případech je [D] nahrazeno ∂ [ε (X, t)] / ∂t, kde [ε] je tenzor s malými kmeny, ∂ / ∂x s ∂ / ∂X ve všech rovnicích a [σ *] s ∂ [σ (X, t)] / ∂t. Poslední dva kroky nelze vždy odůvodnit, a to ani v případě velmi malého přetvoření, kdy například u materiálu nezávislého na rychlosti není dσ / dε p ve srovnání s σ velké, nebo pokud se rychlost otáčení vláken materiálu může výrazně zvýšit. než míry natahování, což je problémem se vzpěrami iu čistě elastických pevných látek.