Tenzorová analýza, odvětví matematiky týkající se vztahů nebo zákonů, které zůstávají v platnosti bez ohledu na systém souřadnic používaný k určení množství. Takové vztahy se nazývají kovariantní. Tenzory byly vynalezeny jako rozšíření vektorů pro formalizaci manipulace s geometrickými entitami vznikajícími při studiu matematických variet.
Vektor je entita, která má velikost i směr; je reprezentovatelný kresbou šipky a kombinuje se s podobnými entitami podle zákona o rovnoběžníku. Kvůli tomuto zákonu má vektor komponenty - pro každou souřadnicovou soustavu jinou sadu. Když se změní souřadný systém, změní se složky vektoru podle matematického zákona transformace, které lze odvodit z paralelogramového zákona. Tento zákon transformace složek má dvě důležité vlastnosti. Zaprvé, po sledu změn, které skončí v původním souřadném systému, budou složky vektoru stejné jako na začátku. Za druhé, ve složkách budou přítomny vztahy mezi vektory - například tři vektory U, V, W, takže 2U + 5V = 4W - bez ohledu na souřadný systém.
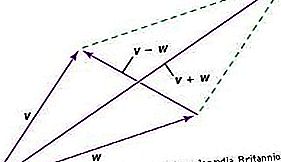
Vektor tedy lze považovat za entitu, která má v n-dimenzionálním prostoru n složky, které se transformují podle specifického zákona o transformaci mající výše uvedené vlastnosti. Samotný vektor je objektivní entita nezávislá na souřadnicích, ale je s ním nakládáno z hlediska komponent se všemi souřadnými systémy na stejném základě.
Bez naléhání na obrazový obraz je tenzor definován jako objektivní entita, která má komponenty, které se mění podle transformačního zákona, který je generalizací vektorového transformačního zákona, ale který si zachovává dvě klíčové vlastnosti tohoto zákona. Kvůli pohodlí jsou souřadnice obvykle očíslovány od 1 do n, a každá složka tenzoru je označena písmenem majícím horní a dolní index, z nichž každý nezávisle převezme hodnoty 1 až n. Tak tensor zastoupené součásti T ab c by mít n 3 komponenty jako hodnoty a, b, a c běh od 1 do n. Skaláry a vektory představují zvláštní případy tenzorů, z nichž první má pouze jednu složku na souřadný systém a druhý má n. Každý lineární vztah mezi tenzoru komponenty, jako as7R BCD + 2s se BCD - 3T je BCD = 0, je-li platná v jednom souřadnicovém systému, platí ve všech a představuje tak vztah, který je objektivní a nezávislá na souřadnicových systémů i přesto, že nedostatek obrazové reprezentace.
Zvláště zajímavé jsou dva tenzory, nazývané metrický tenzor a tenzor zakřivení. Metrický tenzor se používá například při přeměně vektorových komponent na velikosti vektorů. Pro jednoduchost zvažte dvojrozměrný případ s jednoduchými kolmými souřadnicemi. Ať vektor V mají složky V, 1, V 2. Pak podle Pythagorovy věty aplikován na pravý trojúhelníku OAP čtverec velikosti V je daný byOP 2 = (V 1) 2 + (V 2) 2.

V této rovnici je skrytý metrický tenzor. Je skrytý, protože se zde skládá z 0 a 1, které nejsou zapsány. Pokud je rovnice přepsána ve formátu 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, je zřejmá celá sada komponent (1, 0, 0, 1) metrického tenzoru. Jsou-li použity šikmé souřadnice, má vzorec pro OP 2 obecnější tvarOP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, množství g 11, g 12, g 21, g 22 jsou nové komponenty metrického tenzoru.
Z metrického tenzoru je možné vytvořit složitý tenzor, nazývaný tenzor zakřivení, který představuje různé aspekty vnitřní zakřivení n-rozměrného prostoru, do kterého patří.
Tenzory mají mnoho aplikací v geometrii a fyzice. Při vytváření své obecné teorie relativity Albert Einstein tvrdil, že fyzikální zákony musí být stejné bez ohledu na to, jaký souřadnicový systém se používá. To ho vedlo k vyjádření těchto zákonů z hlediska tenzorových rovnic. Z jeho speciální teorie relativity již bylo známo, že čas a prostor jsou tak úzce propojeny, že tvoří nedělitelný čtyřrozměrný prostorový čas. Einstein předpokládal, že gravitace by měla být zastoupena pouze z hlediska metrického tenzoru čtyřrozměrného časoprostoru. Aby vyjádřil relativistický gravitační zákon, měl jako stavební bloky metrický tenzor a tenzor zakřivení z něj vytvořený. Jakmile se rozhodl omezit na tyto stavební bloky, jejich nízká nedostatek ho vedl k v podstatě jedinečné tenzorové rovnici pro zákon gravitace, ve které gravitace nevznikla jako síla, ale jako projev zakřivení časoprostoru.
Zatímco tenzory byly studovány dříve, byl to úspěch Einsteinovy obecné teorie relativity, která vyvolala současný rozšířený zájem matematiků a fyziků o tenzory a jejich aplikace.