Riemannova hypotéza, v teorii čísel, hypotéza německého matematika Bernharda Riemanna o umístění řešení funkce Riemanna zeta, která je spojena s teorémem prvočísla a má důležité důsledky pro distribuci prvočísel. Riemann zahrnul hypotézu do noviny „Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse“ („O počtu prvočísel méně než dané množství“), zveřejněné v listopadu 1859 vydání Monatsberichte der Berliner Akademie („Měsíční přehled“ Berlínské akademie “).
Funkce zeta je definována jako nekonečná řada ζ (s) = 1 + 2 −s + 3 −s + 4 −s + ⋯, nebo, v kompaktnějším zápisu, , kde sčítání (Σ) termínů pro n běží od 1 do nekonečna přes kladná celá čísla as je fixní kladné celé číslo větší než 1. Funkce zeta byla nejprve studována švýcarským matematikem Leonhardem Eulerem v 18. století. (Z tohoto důvodu se to někdy nazývá Eulerova zeta funkce. Pro ζ (1) je tato řada jednoduše harmonickou řadou, známou od starověku, aby se zvětšovala bez omezení - tj. Její součet je nekonečný.) Euler dosáhl okamžité slávy, když ukázal v roce 1735, že ζ (2) = π 2 /6, je problém, který unikl největší matematiky éry, včetně rodu švýcarský Bernoulliho (Jakob, Johann, a Daniel). Obecněji, Euler objevil (1739) vztah mezi hodnotou funkce zeta pro sudá celá čísla a Bernoulliho čísly, které jsou koeficienty v Taylorově řadě rozšíření x / (e x - 1). (Viz také exponenciální funkce.) Ještě úžasnější, v roce 1737 Euler objevil vzorec vztahující se k funkci zeta, který zahrnuje sčítání nekonečné posloupnosti termínů obsahujících pozitivní celá čísla a nekonečný produkt, který zahrnuje každé prvočíslo:
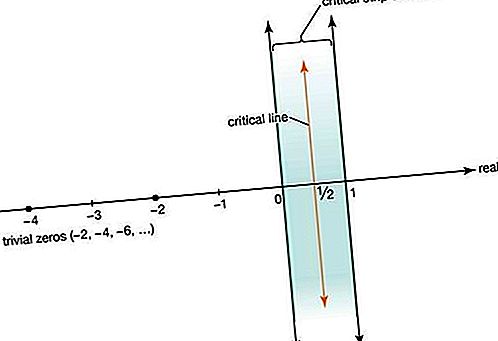
Riemann rozšířil studium funkce zeta tak, aby zahrnovala komplexní čísla x + iy, kde i = druhá odmocnina √ 1, s výjimkou přímky x = 1 v komplexní rovině. Riemann věděl, že funkce zeta se rovná nule pro všechna záporná sudá celá čísla −2, −4, −6,
(tzv. triviální nuly) a že má v kritickém proužku komplexních čísel nekonečný počet nul, které striktně spadají mezi řádky x = 0 a x = 1. Věděl také, že všechny netriviální nuly jsou symetrické s ohledem na kritická řádek x = 1 / 2. Riemann usoudil, že všechna netriviální nula jsou na kritické linii, dohad, který se následně stal známým jako hypotéza Riemanna.
V roce 1914 anglický matematik Godfrey Harold Hardy se ukázal jako nekonečný počet řešení £ (s) = 0 existují na kritické hranici x = 1 / 2. Následně různí matematici ukázali, že velká část řešení musí ležet na kritické linii, i když časté „důkazy“, že na nich jsou všechna netriviální řešení, jsou vadné. Počítače byly také použity k testování řešení, přičemž prvních 10 bilionů netriviálních řešení leží na kritické hranici.
Důkaz Riemannovy hypotézy by měl dalekosáhlé důsledky pro teorii čísel a pro použití prvočísel v kryptografii.
Riemannova hypotéza byla dlouho považována za největší nevyřešený problém v matematice. Byl to jeden z 10 nevyřešených matematických problémů (23 na tištěné adrese), které německý matematik David Hilbert představil jako výzvu pro matematiky 20. století na druhém mezinárodním kongresu matematiky v Paříži 8. srpna 1900. V roce 2000 americký matematik Stephen Smale aktualizoval Hilbertovu myšlenku seznamem důležitých problémů pro 21. století; Riemannova hypotéza byla číslo jedna. V roce 2000 to bylo určeno Millennium Problem, jeden ze sedmi matematických problémů vybraných Clay Mathematics Institute of Cambridge, Massachusetts, USA, pro zvláštní ocenění. Řešení pro každý problém tisíciletí stojí 1 milion dolarů. V roce 2008 ji agentura pro obranný výzkum USA (DARPA) uvedla jako jeden z DARPA Mathematical Challenges, 23 matematických problémů, pro které požadovala výzkumné návrhy na financování - „Mathematical Challenge Devatenáct: Vypořádat hypotézu Riemanna. Svatý grál teorie čísel. “